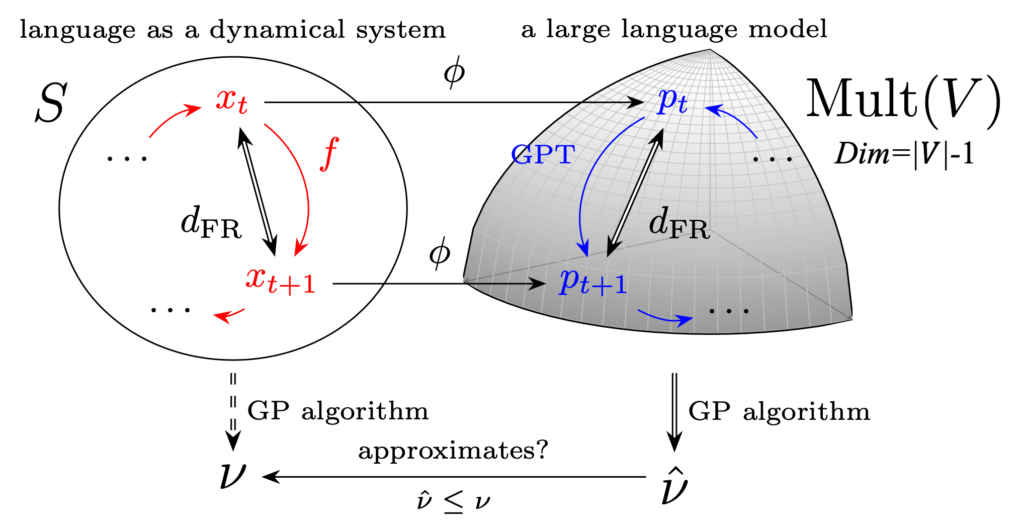
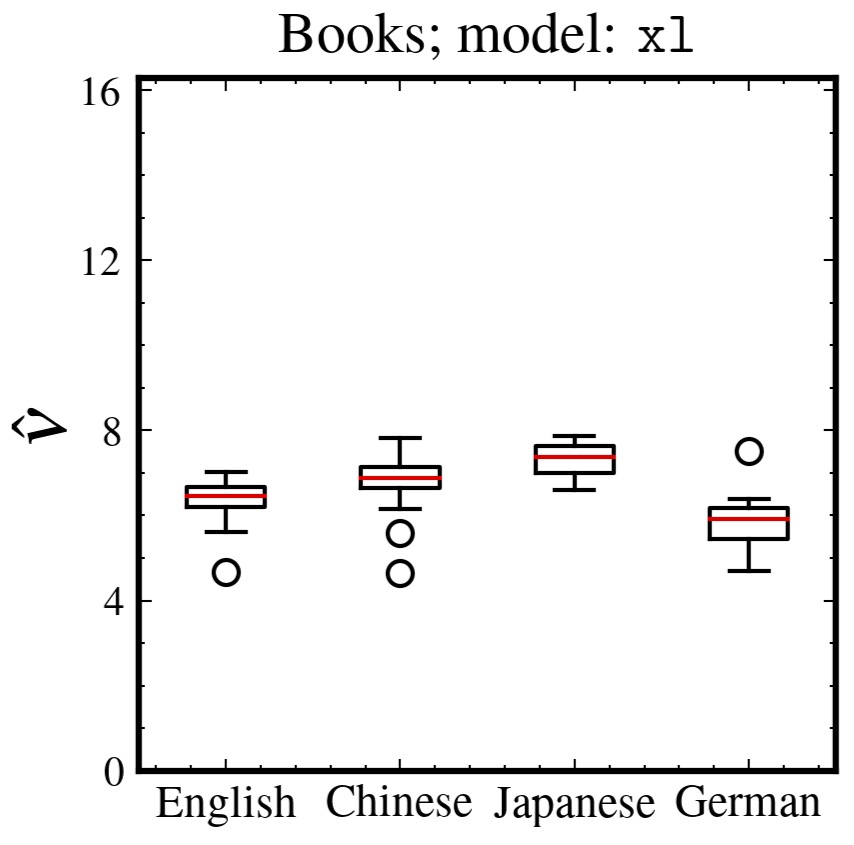
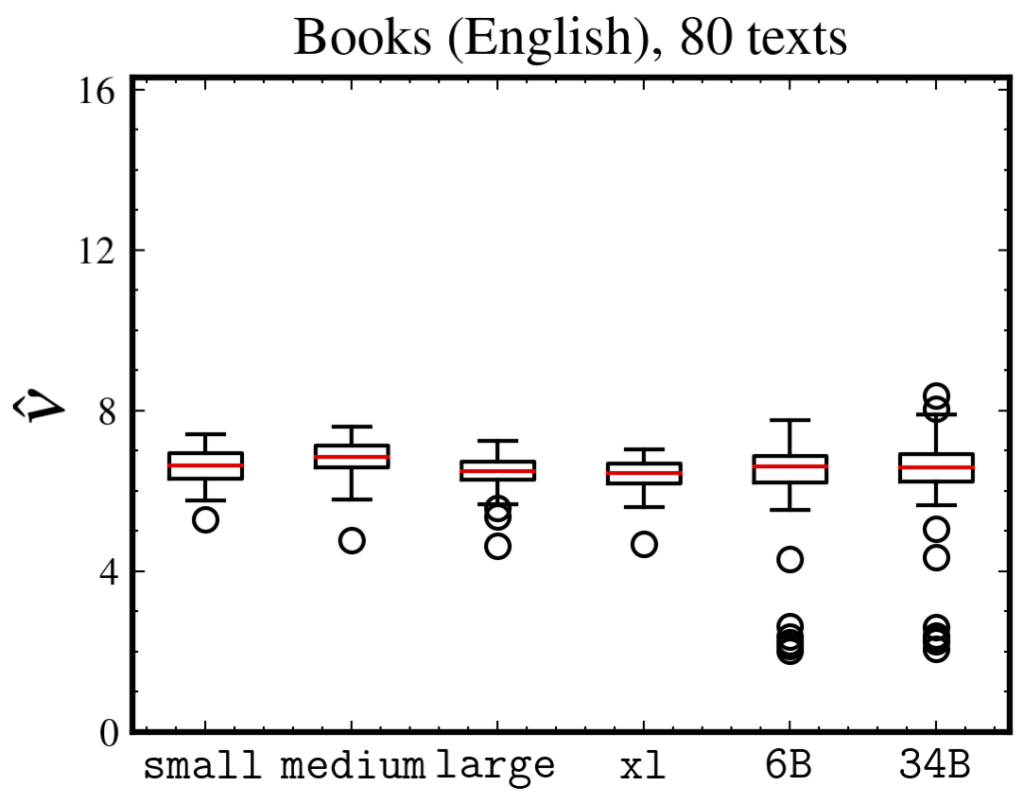
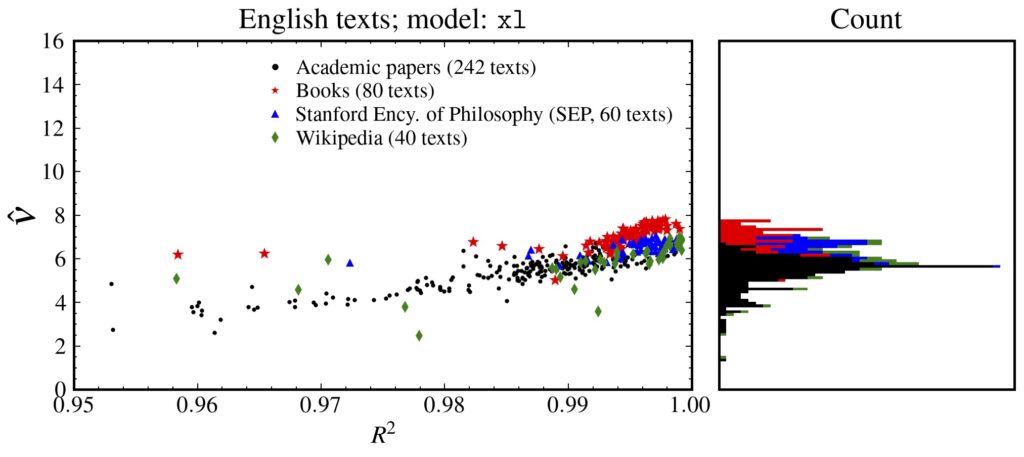
The correlation dimension of natural language is measured by applying the Grassberger-Procaccia algorithm to high-dimensional sequences produced by a large-scale language model. This method, previously studied only in a Euclidean space, is reformulated in a statistical manifold via the Fisher-Rao distance. Language exhibits a multifractal, with global self-similarity and a universal dimension around 6.5, which is smaller than those of simple discrete random sequences and larger than that of a Barabási-Albert process. Long memory is the key to producing self-similarity. Our method is applicable to any probabilistic model of real-world discrete sequences, and we show an application to music data.

System state xt and the next-word probability distribution pt
pt as the image of xt through the marginalization mapping φ
A correlation dimension of ~6.5 is observed across languages
The correlation dimension value is stable with respect to the model size of GPT
Distribution of correlation dimension values across texts from different sources.

References

  • Xin Du and Kumiko Tanaka-Ishii. Correlation dimension of natural language in a statistical manifold. Physical Review Research 6, L022028, 2024. [link]

 

Categorized in:

Complex SystemFeaturedLanguage

Tagged in:

, , ,