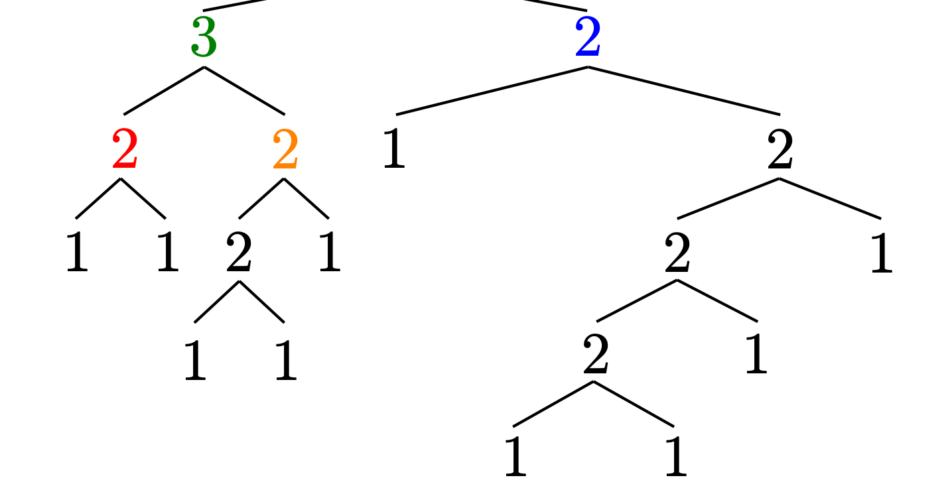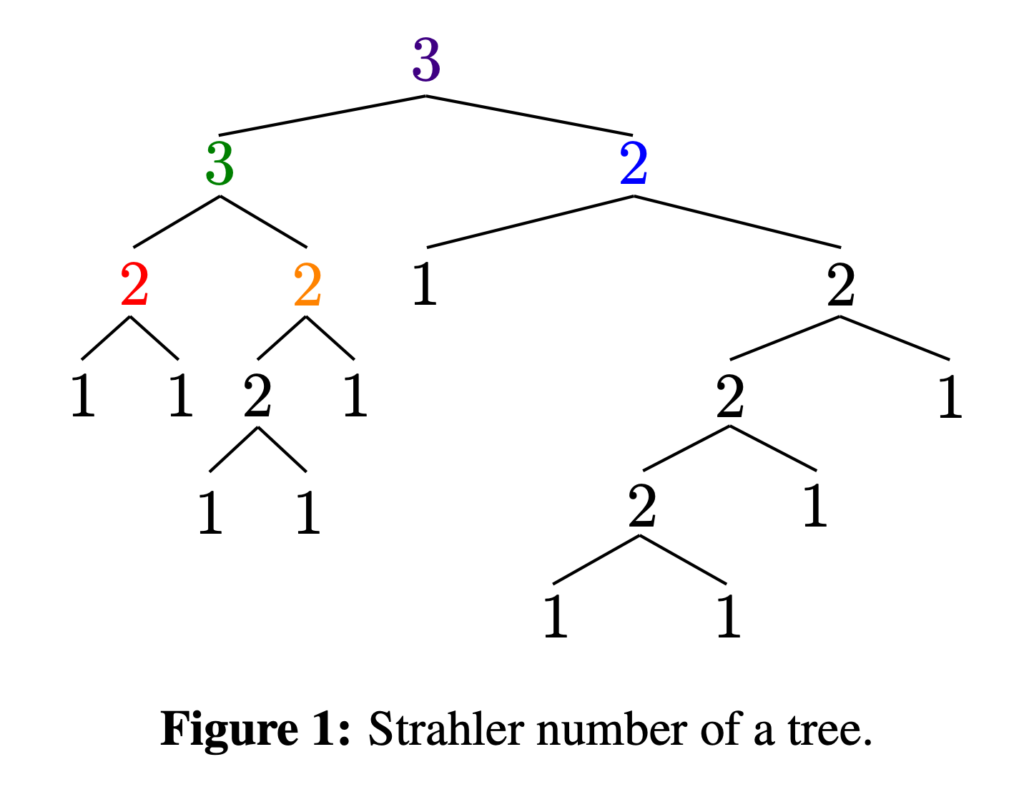
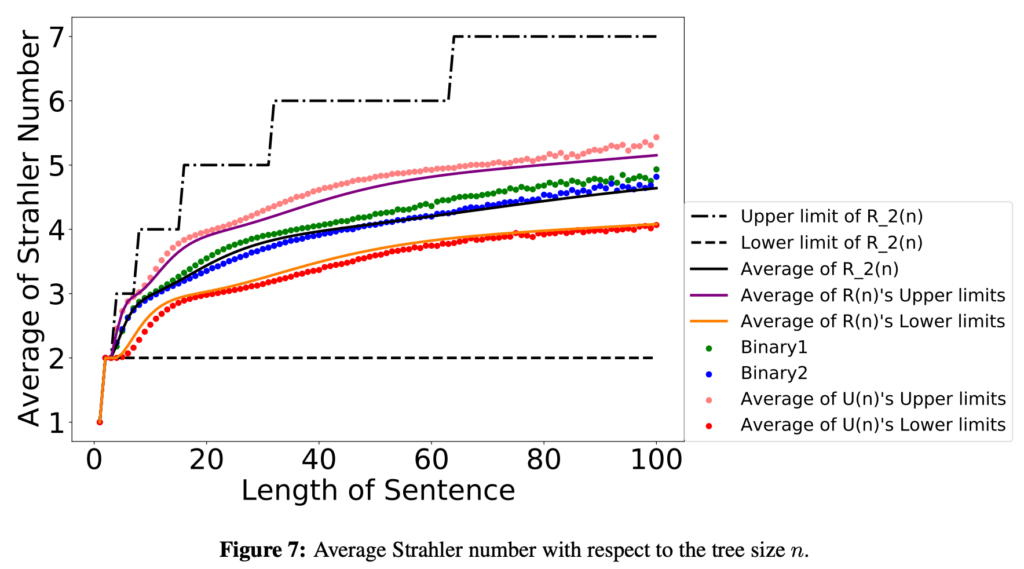
The Strahler number was originally proposed to characterize the complexity of river bifurcation and has found various applications. This article proposes computation of the Strahler number’s upper and lower limits for natural language sentence tree structures. Through empirical measurements across grammatically annotated data, the Strahler number of natural language sentences is shown to be almost 3 or 4, similarly to the case of river bifurcation as reported by Strahler (1957). From the theory behind the number, we show that it is one kind of lower limit on the amount of memory required to process sentences. We consider the Strahler number to provide reasoning that explains reports showing that the number of required memory areas to process sentences is 3 to 4 for parsing (Schuler et al., 2010), and reports indicating a psychological “magical number” of 3 to 5 (Cowan, 2001). An analytical and empirical analysis shows that the Strahler number is not constant but grows logarithmically; therefore, the Strahler number of sentences derives from the range of sentence lengths. Furthermore, the Strahler number is not different for random trees, which could suggest that its origin is not specific to natural language.
Reference